Background
A hashtable is one of a select few datastructures that take the center spotlight when coding games. Other often encountered structures are vectors/dynamic arrays (of course), ring buffers and intrusive linked lists. I will post about some of them in the future, but today is all about our hashtable implementation!
In this post I will present Cuckoo hashing, which we use to implement our hashtable. Cuckoo hashing gets its name from the cuckoo family of birds, where many species lay eggs in other species nests. When a cuckoo chick hatches, it pushes other eggs/chicks out of the nest and gets all the food for herself. Cuckoo hashing works in a similar way: When we insert an key, we kick out any other key we collide with.
Unlike “standard” hashtables, which rely on chaining when they get a hash collision, cuckoo hashing uses something called open addressing. Open addressing means that when we get a hash collision, we try to find a new empty spot for either the key/value pair we are inserting or for the key/value pair that occupies our slot. There are numerous algorithms to try and find alternate slots to insert an element, such as Linear probing, Quadratic probing, Hopscotch hashing, Robin Hood hashing and more. The advantage of open addressing over chaining is that we get much fewer memory allocations and better cache locality. In this blog post we’ll focus on cuckoo hashing, for no other reason than it’s what I started to look into.
Cuckoo Hashtable
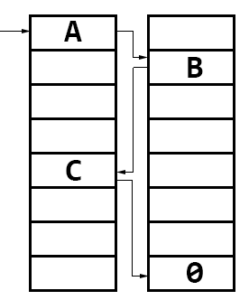
An image depicting a cuckoo path. When we insert something, we collide with A. A will evict B, B evict C, C finds an empty slot so the search terminates.
Cuckoo hashing was first presented by Pagh and Rodler[1] in 2001. Since then it has been further improved by numerous people, however the papers by Fotakis et al[2] and Panigrahy[3] seems to be the the most common cited improvements. But first let’s have a look at the simplest form of cuckoo hashing.
We start by creating a table which is 2*N big, where N is the number of slots we can hash to. We also supply two independent hash functions for our keys. When we later try to insert a key and get a collision, we evict the key occupying the slot. That key is now rehashed using one of our two hashing functions. We then reinsert the evicted key into our table and if we get a collision, we evict the key we collided with and so on. If a certain number of iterations passes and no empty slot is found, we can either resize the table or try to rehash keys with new hash algorithms. This algorithm works fairly well until the table passes a load factor of about 50%.
Improvements
The first paper (by Fotakis[2]) improves cuckoo hashing by increasing the number of hash functions. They show that with 4 independent hash functions, a maximum load factor of 97% is achievable. The second paper (by Panigrahy[3]) instead propose that we divide each slot into multiple sub-slots, thereby making evictions more rare. With this strategy they achieve a maximum load factor of 83.75%. The load factor of the second paper is less than the first, but lookups are cheaper since the structure becomes more cache friendly and fewer hashes needs to be calculated.
By combining the two techniques, we can get a flexible hashtable which we can tweak to our needs. If we use use the naming convention proposed by each author respectively, we can choose to implement a flexible (d,k) cuckoo hashtable, where:
- d is the number of hash functions used. The higher d we have, the higher the maximum load factor.
- k is the number of sub-slots used. Increasing k gives a slightly higher load factor, without sacrificing performance as much.
- Each LOOKUP/DELETE operation looks at most d * k keys. Fitting k keys into as few cache lines as possible gives us better performance.
- The memory footprint of the structure is d * k * N * (sizeof(key) + sizeof(value)) bytes, where N is the number of slots used.
- INSERT can either be modeled as a depth-first search or a breadth-first search. The latter often results in fewer moves of existing elements, which is desirable. I will omit the complexity analysis of the function, but it suffices to say that once we come close to the maximum load factor, we will start to move a lot of key/value pairs around and performance suffers.
A normal cuckoo hashtable could then be expressed as a (2,1) hashtable, Fotakis implementation would be a (4,1) hashtable and Panigrahy’s a (2,2) hashtable.
Performance
I haven’t done any extensive testing on the performance on my implementation of the cuckoo hashtable, for a couple of reasons:
- Lack of real world data – I have tried the performance on a couple of highly artificial cases, so while we can get a feel for the performance it still doesn’t reflect real world usage.
- Lack of optimization – I haven’t yet spent any time on profiling and performance tests, so the numbers I present are probably suboptimal.
- Incomplete implementation – I still haven’t implemented a rehash function, so comparing with an implementation that has that ability is sort of comparing apples to oranges.
Still, I will share some numbers, just take them with a grain of salt. Compiled using /Ox /LTCG in Visual Studio 2015, using (d = 4, k = 2, N = 7919) and a key/value pair of string/string:
- For low loads ( <~50% load factor), inserts are usually 10%-50% faster than std::unordered_map. Lookups are sometimes faster, sometimes slower. This could be due to std::unordered_map doing a rehash of keys at certain intervals, causing insertion times to rise and lookup times to drop.
- For medium loads ( <~80% load factor), the implementations have about the same insert performance, while std::unordered_map having slightly better lookup speed.
- When we nearly saturate the hashtable, insertions can become as much as 5x more expensive than std::unordered_map. Lookups are about ~20% more expensive than std::unordered_map.
- For me, the most impressive figure is how long it takes before we actually fail an insertion. For example, using 63352 (= d * k * N) keys named “test0” to “test63351”, our first failure appears when we try to insert “test62939”. This means that we managed to insert 99.3% of all keys before our first failure. During this test, a total of 186 keys failed in total, giving us a load factor of 99,7%.
Conclusion
The main benefits of cuckoo hashing is that it’s a really space efficient structure. In my implementation, there’s zero bytes overhead per key/value pair. In order to know if a slot is empty, the user needs to supply a null element. This is of course a restriction in the design, but I believe it will work well in practice. Usually you can identify such an element without problem, such as an empty string or 0, -1, INT_MAX etc. With the guaranteed upper bound lookup of d * k inspected elements, the structure is quite impressive. While insertions definitely takes longer when we near maximum load factor, they aren’t unbearably slow.
However, were I to implement an open addressing hashtable again, I would look toward hopscotch hashing or Robin Hood hashing. My guess is that they show a bit better performance, especially for lookups. But our hashtable is fully functional, so improving upon it will have to wait until we actually need to.
There’s also a concurrent implementation of a C++ cuckoo hashtable called libcuckoo, if you feel like trying it out.
